title: 概率论与数理统计笔记
date: 2022-09-05 09:00:00
categories:
- 学习
tags: - 概率论与数理统计
概率论与数理统计
南京大学计算机科学与技术系2022秋课程 概率论与数理统计 个人笔记
欢迎批评补充,学术交流,您可以邮件联系我(邮箱见页面底端)
课程名:
概率论与数理统计
英文名:
Probability and Mathematical Statistics
建议教材:
《概率论与数理统计》,傅冬生等编,科学出版社,2014.
教学周历:
| 周次 | 教学内容 | 教师 | 授课方式 | 备注 |
|---|---|---|---|---|
| 1 | 第一章.随机事件与概率 §1.随机事件及其运算 §2.事件的概率与性质 §3.古典概率 | 傅冬生 | 课堂教学 | 2022年9月5日 |
| 2 | 第一章.随机事件与概率 §4.几何概率 §5.条件概率 §6.独立性 | 傅冬生 | 课堂教学 | 2022年9月19日 |
| 3 | 第一章.随机事件与概率 §7.独立重复试验 第二章 随机变量及其概率分布 §1 随机变量及其分布函数 | 傅冬生 | 课堂教学 | |
| 4 | 第二章 随机变量及其概率分布 §2 离散型随机变量及其分布函数 §3 连续型随机变量及其分布 | 傅冬生 | 课堂教学 | |
| 5 | 第二章 随机变量及其概率分布 §4 随机变量函数的分布 第三章 随机向量及其概率分布 §1 二维随机向量及其分布函数 | 傅冬生 | 课堂教学 | |
| 6 | 第三章 随机向量及其概率分布 §2 二维离散型随机向量 §3 二维连续型随机向量 | 傅冬生 | 课堂教学 | |
| 7 | 第三章 随机向量及其概率分布 §3 二维连续型随机向量 §4 二维随机向量函数的分布 | 傅冬生 | 课堂教学 | |
| 8 | 第四章 随机变量的数字特征 §1 数学期望 §2 方差与矩 | 傅冬生 | 课堂教学 | |
| 9 | 第四章 随机变量的数字特征 §2 方差与矩 §3 协方差与相关系数 | 傅冬生 | 课堂教学 | |
| 10 | 第五章 极限理论 §1 大数定律 §2 中心极限定理 | 傅冬生 | 课堂教学 | |
| 11 | 第六章 统计基础 §1 总体与样本 §2 统计量与抽样分布 | 傅冬生 | 课堂教学 | |
| 12 | 第六章 统计基础 §3正态总体的抽样分布 第七章 参数估计 §1 矩估计 | 傅冬生 | 课堂教学 | |
| 13 | 第七章 参数估计 §2 极大似然估计 §3 估计量的评价标准 | 傅冬生 | 课堂教学 | |
| 14 | 第七章 参数估计 §4 区间估计 第八章 假设检验 §1 假设检验的基本概念 | 傅冬生 | 课堂教学 | |
| 15 | 第八章 假设检验 §2 正态总体均值的假设检验 §3 正态总体方差的假设检验 | 傅冬生 | 课堂教学 | |
| 16 | 第八章 假设检验 §3 正态总体方差的假设检验 §4 分布拟合检验 | 傅冬生 | 课堂教学 |
绪论

1. 随机事件及其运算
一. 随机试验 样本空间 随机事件
1.随机试验
日常生活和社会实践中的两类现象:确定性现象和随机现象。
具有不确定性(或偶然性)的现象称为随机现象。
把对某种随机现象的一次观测或测量称为一个试验。
2. 样本空间(sample space)
将随机试验E的所有可能结果组成的集合称为样本空间,
样本空间的元素,即E的每个结果,称为样本点(或基本事件)
3.随机事件(random occurrence)
基本事件: 一个样本点组成的单点集,不可再分.
随机事件: 称试验E的样本空间L的子集为E的随机事件,记作A,B, C等等;
eg: 事件A:出现偶数点,A={2, 4, 6}
随机事件发生:该事件所包含的一一个样本点在试验中出现。
两个特殊的事件:
必然事件:样本空间本身;
不可能事件:空集
二、事件间的关系与运算
I. 关系
1) 包含关系B>A
如果A发生必导致B发生,
2) 互斥关系
n个事件互斥
3)相等关系
II. 运算
并/交/差/对立


2. 事件的概率及性质
一. 频率的定义和性质
定义:在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数na,称为事件A发生的频数。比值na/n称为事件A发生的频率,并记成f,(A) 。
频率的稳定性
在充分多次试验中,事件的频率总在一个定值附近摆动,而且,试验次数越多,一般来说摆动越小.这个性质叫做频率的稳定性.
公理化的def:

3.等可能概率(古典概型)
有限等可能
1)样本空间有限
2)每个等可能
6.独立性
6.1 性质
1)定义$A,B$满足$P(AB)=P(A)P(B)$,称事件$AB$相互独立
- 理解$P(B|A) = P(B)$
2)概率为0|1 于任意事件

3) 定理:以下情形等价 对称性
- $AB$相互独立
- $\overline{A}B$相互独立
- $A\overline{B}$相互独立
- $\overline{A}\overline{B}$相互独立
4)分组独立性
将上述$n$个事件划分成没有公共事件的$k$组,每组中的事件做任意事件运算,得到的$k$个新事件仍相互独立
*相互独立!=互不相容
证明 见笔记
6.2 多个事件独立

6.21 数量
即任意的$2,3,…,n$个事件拿出来都满足上述等式(共有$C_n^2+C_n^3+…+C_n^n=2^n-n-1个等式$)
6.22 相互独立事件至少发生一个
加法公式简化:$A_i$相互独立,则$P(A_1\bigcup A_2\bigcup…\bigcup A_n)=1-P(\overline{ {A_1}\bigcup{A_2}\bigcup…\bigcup{A_n} })= 1-P({\overline{A_1}\bigcap\overline{A_2}\bigcap…\bigcap\overline{A_} }})=1-P(\overline{A_1})P(\overline{A_2})…P(\overline{A_n})$
6.23 小概率事件原理
书p19
可靠性
串联 并联
书1.25 笔记两两并再串联
桥式系统
7. 独立重复实验

方差
泊松分布
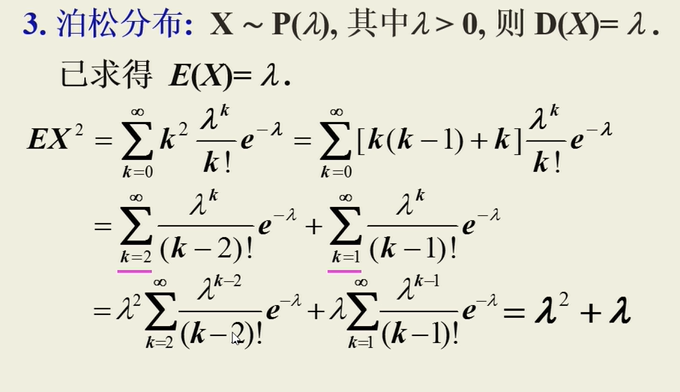
几何分布
